Question 2

Consider the functions $y = f(x)$ and $y = g(x)$, and the regions shaded in the diagram below.

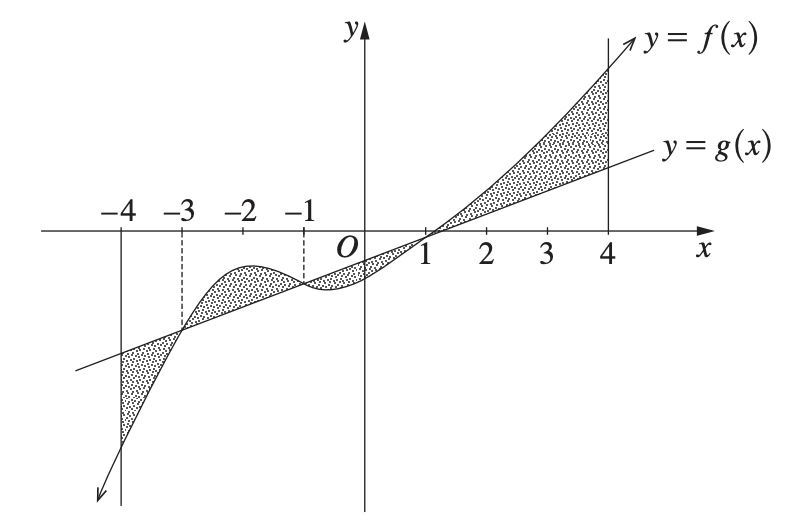
Which of the following gives the total area of the shaded regions?

A. $\displaystyle \int^{4}_{-4} f(x) - g(x) dx$

B. $\displaystyle \left| \int^{4}_{-4} f(x) - g(x) dx \right|$

C. $\displaystyle \int^{-3}_{-4} f(x) - g(x) dx + \int^{-1}_{-3} f(x) - g(x) dx + \int^{1}_{-1} f(x) - g(x) dx \int^{4}_{1} f(x) - g(x) dx$

D. $- \displaystyle \int^{-3}_{-4} f(x) - g(x) dx + \int^{-1}_{-3} f(x) - g(x) dx - \int^{1}_{-1} f(x) - g(x) dx + \int^{4}_{1} f(x) - g(x) dx$

Solution

This is an example of calculating the absolute area between two lines. The region is given by the area $\displaystyle \int^4_{-4} \left| f(x) - g(x) \right| dx$.

...

Log in or sign up to see more